ABC
|
The Add-Subtract Mechanism of the ABC
|
|
|
|
The Add-Subtract Mechanism was a fully-electronic 1-bit binary arithmetic unit. In the white box is an excerpt from Atanasoff's paper about the ABC, describing the ASM and including the original schematic.
Further below is a reorganized version of the schematic, and an equivalent logic diagram drawn with modern gate symbols.
[ Excerpt from ]
Computing System for the Solution of Large Systems of Linear Equations
By John V. Atanasoff
Aug. 1940
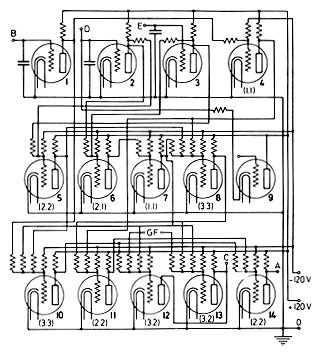
. . .
The vacuum tubes used in the circuit are twin triodes, (type 6C8G). In the drawing, the triodes are indicated separately but only seven envelopes are needed for a single asm. Each triode shifts between two extreme states in the operation of the circuit: the grid in the range from less than -5 volts to a value greater than zero, the plate in the range from 120 volts to a value less than 50 volts when a plate resistor of 50,000 ohms is used. It is found to be advantageous to slightly alter the plate resistor at certain points of the circuit but this is a refinement not needed in an explanation of the circuit.
There are two principal types of circuits in which the tubes are used. The triodes 1, 2, and 3 have their grids connected to small condensers and their potentials do not change until a new charge is placed on these condensers (the triode 2 can also be discharged through the agency of the triode 9). On the other hand, the tubes 4, 5, 6, 7, 8, 10, 11, 12, 13, 14 have resistance networks across their grids consisting of p equal resistors connected to various plates and one resistor connected to the -120V bias supply. A symbol of the type (p,q) will be noticed beside each of the triodes in Fig. 2. This indicates that there are p plate connections to the grids of this triode and that the bias supply resistor is adjusted so that q plates will have to be low, i.e., less than 50 volts, to block this triode. Experience as well as theory shows that when p=3, the largest number used, that the grid of the given tube changes about 12 volts when one of the plates connected to it changes from low to high. This has proved adequate to make the action of the device sharp and clean since a grid swing of only 5 volts is needed. Within a considerable range (which can be easily increased if necessary) the tube characteristics and the values of resistors and other circuit elements make no difference in the results obtained. Comparable remarks are applicable to any computing machine.
By following the diagram and making use of the (p,q) symbols attached to the various triodes, it is easy to verify the following table. In this table H stand for the higher voltage in the range and L for the lower.
| |
Numbers
Presented | Corresp.
Voltage |
Addition
F-high G-low | Subtraction
F-low G-high |
| B D E | B D E | A C | A C |
|---|
| 0 0 0 | H H H | H H | L L |
| 0 0 1 | H H L | L H | L L |
| 0 1 0 | H L H | L H | L L |
| 0 1 1 | H L L | H L | H L |
| 1 0 0 | L H H | L H | L H |
| 1 0 1 | L H L | H L | H H |
| 1 1 0 | L L H | H L | H H |
| 1 1 1 | L L L | L L | L L |
|
The symbols A and C represent the two output terminals. If A is high the corresponding abaci element carries a zero, if A is low a one. Likewise if C is low there is a carry-over into or a borrowing from the next higher place.
In this way the machine rapidly performs the elementary operations of addition and subtraction. Other operations are carried on much as in other calculating machines, the chief difference being that the electrical principle allows greater versatility of operation and control. It will be noted that there are no mechanical oscillations at the computing frequency and so full advantage may be taken of the high speed of the electrical vacuum-tube circuits.
. . .
|
|
Atanasoff's comment about taking full advantage of the high speed is curious. It is true as it relates to the ASM in isolation, but the use of the ASMs in the ABC machine was still (very) limited by the mechanical revolution of the drums.
In short, different values of the grid resistors achieved different types of gates (NAND/NOR/NOT).
In the expressions (p,q), p is the number of inputs to the gate, q is the number of inputs which must be 1 to send the output to 0. So (2,2) is a 2-input NAND gate, (2,1) is a 2-input NOR gate. Note that negative logic is used: 1=L (lower voltage), 0=H (higher voltage).
|
Figure 1: Reorganized schematic of the ABC Add-Subtract Mechanism
|
|
|
An Assessment of the Gate Design (added Aug 2008)
| |
Table 1:
Summing Point Voltages
for 3-Input Gate
|
| Inputs |
Voltage |
| 0 0 0 | v0 |
| 0 0 1 | v1 |
| 0 1 0 | v1 |
| 0 1 1 | v2 |
| 1 0 0 | v1 |
| 1 0 1 | v2 |
| 1 1 0 | v2 |
| 1 1 1 | v3 |
|
|
|
While this approach to gate design has a certain appeal in principle, in practical engineering terms it has some shortcomings.
As Atanasoff mentions, some variation and manual selection of resistors at points in the network were required in the ASM.
As can be seen in Figure 1 above, the gate design relies on a resistive summing point, followed by a single non-linear device, to produce the binary logic function.
Design values and component tolerance requirements are tight because different logic states at the inputs produce a range of voltage levels at the summing point which the tube must then change into just two voltage levels at the plate (saturation and cutoff).
Depending on what type of logic function is to be achieved, the mapping of the set of summing point voltages to two output voltages differs.
Table 1 shows this for a 3-input gate.
The tube grid will see 4 different voltage levels (v0,v1,v2,v3) for the 8 input states:
For negative logic:
v3 < v2 < v1 < v0
NAND: v3 < Vgc and Vgs < v2 < v1 < v0
NOR: v3 < v2 < v1 < Vgc and Vgs < v0
Vgc = grid voltage required for tube cutoff (approx. -5V)
Vgs = grid voltage required for tube saturation (approx. 0V)
|
| |
|
Figure 2: Transfer Characteristics of a 6C8
|
|
|
|
The requirements are compounded by the fact that tube characteristics around saturation are fairly soft or curved.
Figure 2 shows a graph of the plate voltage vs. grid voltage as measured for one triode of a 6C8 with a plate resistor of 50K, B+ of 110 or 120V, and a 220K resistor between the grid and the variable input voltage source.
Note that once the grid goes positive, the plate voltage still shows considerable variation, in contrast to the comparitively sharp corner around cutoff.
Particularly in the case of the (negative logic) NAND gate - where several grid voltages must produce tube saturation - the actual result will be a range of plate voltages, rather than a uniform 'logic 1' level desired.
Subsequent, or more modern, logic designs (including RTL) avoid the range of summing point levels by having non-linear devices on each input before being combined, so there are essentially only two levels at the summing point, regardless of logic function and the number of inputs.
| |
|
Figure 3: Modern logic equivalent of the ABC Add-Subtract Mechanism
|
|
|
|
Modern Logic Equivalent
The ASM design can be expressed in terms of modern boolean logic gates with the exception of gates 12 and 13, as shown in Figure 3.
Gates 12 and 13 function as inverting three-input majority-logic gates (if any two or more inputs are 1 the output is 0) and would be compound gates in boolean formulation.