|
|
The function execution state machine implements several procedures:
|
These procedures are executed from within a main loop as shown in figure 1. The idle state is state 0. When the function latch (U) is loaded with a non-zero code value or the F54 flag is 1 the function execution state machine leaves idle and begins executing a procedure. The procedure selection is made by the function code, the FMUL, FDIV, F54 and FN flags and the memory mode switches.
As the idle state is left, the DP counter is set to 2 (actually done by the T state machine leaving TSDISP+FETCH). The multiply, divide and square root procedures will use DP as a loop counter, having it at 2 means it can be incremented 14 times before it hits 0 again, 14 being the number of numeric digits in a register.
With the exception of the clearing procedures and accumulating into one of the 4 memory registers, all the procedures leave their result in Y (or M1-M4 for U=MEMGET) and finish by going through state 21 to copy the result into X for display, before returning to idle. If the number is negative it is in 10s-complement form in Y (or Mn) and this is detected during the pass through state 21 via the W0 flag which last captured the zero-state of the sign digit. If the sign is not zero, the FNEG flag is set to 1, the state loops on itself and as a consequence of FNEG now being 1, CARSUB is enabled, and the number in Y is negated as it passes through the arithmetic unit to be written out to X again. The sign digit of X is now zero so the loop exits and the FNEG flag results in the NEGATIVE lamp being turned on in the display.
| Figure 1: The Main Loop |

|
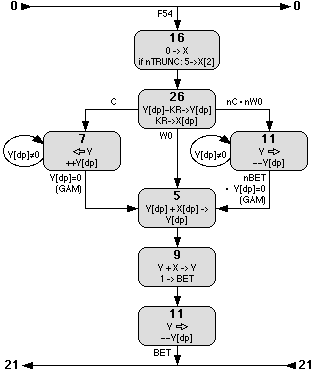
The clearing procedures are very simple, producing one state cycle, in which X and/or Y register digits are filled with zeroes.
Most of the effort in addition and subtraction goes to aligning the decimal points. Throughout this procedure if the function is memory-accumulate the applicable M1-4 register is substituted for the Y register. At the end of the procedure, if accumulate nothing more need be done and the process returns directly to idle. For addition and subtraction, the result is in Y and the process heads for state 21 for display and possible negation.
State 26: The decimal point positions of the two operands are compared and one of the three branches is taken for less-than, equal, or greater-than.
States 7,19: One of the two operands is shifted up until they are in alignment. There is no overflow detection if an operand being shifted is too large for the shift. Y[dp] is the count of how many shifts to perform.
States 25,5: X[dp] is the final decimal position and is copied to Y in state 5 (Y[dp] is 0 when state 5 is entered). State 25 adjusts X[dp] with the difference if necessary.
State 9: The actual addition or subtraction is finally performed. For subtraction or addition of negatives, Y is already in signed form and so does not have to adjusted. If subtraction was requested, the FNEG flag is set which will enable negation during the addition. FNEG may already have been set if X was negative.
Memory-Retrieve simply heads straight to state 21 where the desired M1-4 register, instead of Y, is copied to X for display.
For Memory-Save, the X register is copied to the desired M1-4 register. If the displayed number is negative, FNEG is 1 so the number will be negated as it passes through the arithmetic unit to be written to the M1-4 register.
| Figure 5: The Rounding Procedure | |
|
The rounding procedure is very similar to the alignment steps in addition/subtraction.
State 16: If round-off is requested, as opposed to truncation (via the 5/4 switch on the keyboard), a 5 is loaded into the LSD of X.
States 26,7,11,5: State 26 compares the decimal point position of the number with the number of digits selected by the rounding switch (KR) on the keyboard and a branch taken based on the difference. The number is shifted up or down as per the difference. State 5 effectively copies X[dp], which was set to KR in state 26, to Y[dp].
States 9,11: X is added in to accomplish the (potential) round-up from the LSD, and the LSD is then discarded by shifting right.
Note that as state 11 is used in two different places in this procedure, the two uses must be distinguished as they exit to different states.
The BET flag is used to direct the exit, being set to 1 in state 9.
There are two procedures involved in multiplication. When the multiplication key is pressed (U=MUL), the displayed number (X) is saved in Y, and the FMUL flag is set so that a later press of the add or subtract keys will invoke the multiplication procedure (UMAS) rather than addition/subtraction.
During the multiplication procedure, X will be the multiplicand, Y will be the multiplier (shifted to the higher digits), and the product will accumulate in the lower digits of Y.
| Figure 6: The Multiplication Procedures |

|
2. State 5: The final decimal point is calculated in a decimal-point-only state cycle.
3. States 4,9 loop: In state 4 the multiplier (Y) is shifted up until a non-zero numeral appears in the uppermost digit of the register. The process then switches to the addition loop (state 9), with repeated additions of the multiplicand (X) accumulating in the lower digits of Y. Of course it is possible that the additions will overwrite the lower digits of the multiplier already in Y, but this only occurs if the result will be an overflow anyways.
Each addition also results in the uppermost digit of the multiplier (Y) being decremented due to the addition of the 9 which was previously loaded into X in state 3. As this takes place in the uppermost digit, the resultant carry is of no consequence.
When the uppermost digit of the multiplier is decremented to 0 the addition loop exits and the process returns to state 4. The multiplier, along with the accumulating product (both in Y) are shifted until a non-zero numeral again shows up to take it back to the addition loop, or the loop counter (DP) is exhausted to finish the process. Recall that the DP counter was primed with 2 back when leaving the idle state, so there are 16-2=14 iterations through state 4.
See also: Multiplication example.
As with multiplication there are two procedures involved in division. When the divide key is pressed (U=DIV), the displayed number (X) is shifted to the high end of the register and transferred to Y, and the FDIV flag is set so that a later press of the add or subtract keys will invoke the division procedure (UDIV) rather than addition/subtraction.
During the division procedure, X will be the divisor, and Y will be the dividend. For some reason the designers chose to use a third register (memory M2) in which to build the quotient, so M2 is useless to the user across divisions. Most calculators of this vintage manage to accomplish division using just two registers.
The basic division is a straightforward long division process, with the dividend shifted up for resolution, the divisor similarly shifted up, followed by repeated subtractions of the divisor from the dividend, and shifts of the dividend and quotient as subsequent upper digits of the dividend are eliminated by the subtractions.
| Figure 7: The Division Procedures | |

|
2. State 26: An initial decimal point is calculated.
3. States 19,20: The divisor is shifted to the high end of the register, but not into the sign digit.
4. States 22,14 loop: The divisor is repeatedly subtracted from the dividend with the quotient building in M2 by incrementing the decimal point digit. The loop exits when the subtractions send the divisor negative.
6. States 9,28,7: The overdraft from the last subtraction is corrected and the now-smaller dividend and the quotient are shifted up. Some special logic during state 28 provides for the decimal point digit of M2 to be shifted left into the LSD of the register. The loop counter (DP) is incremented and the procedure finishes when it hits 0 or when it becomes apparent that the decimal point will go too far to the left.
7. States 13,6: The quotient is copied to Y. The decimal point was already calculated into Y, so the decimal point digit is not copied during state 6.
The more tedious aspect of the process to follow is the derivation of the decimal point position.
The essential decimal point calculation is made by the subtraction of the decimal point positions in state 26.
The other adjustments to the decimal point in states 24,20,19 and 7 are to track the decimal point with the shifting of the registers.
The tests in states 19 and 7 involving the GAMma flag are to terminate the process early in situations where continuing would result in the decimal point of the quotient ending up too far to the left:
1/1 = 0 1.0 0 0 0 0 0 0 0 0 0 0 0 is OK 1/10 = 0.1 0 0 0 0 0 0 0 0 0 0 0 0 is not permitted for some reason 1/100 = .0 1 0 0 0 0 0 0 0 0 0 0 0 0 is not possible to display instead: 1/10 = 0 0.1 0 0 0 0 0 0 0 0 0 0 0 1/100 = 0 0.0 1 0 0 0 0 0 0 0 0 0 0 |
See also: Division example.
Square root involves the "sum of odd numbers" method, with multiplying the number by 5, repeatedly subtracting the building root while a digit of the root is incremented. If N is the number whose root is desired and R is it's root then:
1 = 1^2 = 1
4 = 2^2 = 1 + 3
9 = 3^2 = 1 + 3 + 5
N = R^2 = sum[i=1..R] of ( 2i - 1 )
5*N = 5*(R^2) = sum[i=1..R] of ( 10i - 5 )
In other words, (one way) to find the root of a number is to figure out how many sequential odd numbers must be added together to produce the number. To obtain resolution for small numbers the number can be multiplied by a multiple of 100 via shifting, so the root will be the equivalent multiple of 10:
N*(100^i) = ( R*(10^i) )^2
Digits of the root are derived one-by-one from the MSD down to the LSD by repeated subtractions of a constructed value from N. At any time the constructed value being subtracted looks like
...rrrd5000...
where r are digits of the root which have already been resolved and d is the digit being resolved.
See also: Description of Friden SRW procedure at the Museum of HP Calculators.
| Figure 8: The Square Root Procedure | |

|
2. States 24,20: The number is shifted up to the high end of register X, then shifted back down 1 or 2 digits as necessary to be a multiple of 100 (because SQRT(100)=10 and SQRT(10)=3.etc). This also guarantees an empty digit at the upper end of the register so that operations later will not cause an overflow.
3. States 4,1,11 loop: An initial decimal point is calculated.
During each loop iteration Y[dp] is decremented once for every two X[dp] increments.
At the exit of the loop
4. State 9 loop: The intention here is to multiply the number by 5. Recall the DP counter was set to 2 back when the T state machine left the TSDISP state. The state 9 loop iterates until DP hits 7, so now Y=5*number (7-2=5).
5. Transient actions: Two additional actions are performed when the DP counter hits 7, the function code is changed from 12 (SQRT1) to 13 (SQRT2) by setting the 1 bit in the U latch, and the DP counter is set to 3 by clearing bits 4 and 8 of the DP counter. The DP counter will be used as a loop counter and a position index. As a position index it will determine the appropriate digit in which to inject a "5" and which digit to increment in the building root. It starts at 3 to account for the guard digit and even/odd alignment at the upper end of the register established back in states 20 and 24.
6. State 13: X is cleared. The root will build in X.
7. States 22,3 loop: The building root is repeatedly subtracted from the number. A "5" is injected at the appropriate digit through the B latch during the subtraction, and the appropriate digit is incremented, all until a borrow occurs from an overdraft from the number.
The 'appropriate digit' is determined by cycling the DP counter during the number cycle and watching when it hits 0 or 1. It returns to the same value at the end of the number cycle because both the number cycle and DP counter are base 16, but the DP counter's phase relative to the number (DGT) shifts during the procedure.
8. States 9,7 loop: The overdraft is corrected, and the number (Y) (now a digit smaller from the subtractions) is shifted up. The DP counter is incremented so the next-digit-down is targeted in the following 22,3 loop.
9. States 20,6: An additional right shift of the constructed root is performed and the result copied to Y. The previously calculated decimal point is already in the Y register, so the DP digit is not copied.
See also: Square Root example.
|
Examples
Architecture | Electronics | Arithmetic | Timing | T States | States | Procedures | Numeral-Entry Casio AL-1000 Technical Description EEC |
bhilpert Nov 2004 |